cs231n Lecture4 introduction to Neural Network

abstract

4강에서는 주로 Optimization의 기반이 되는 과정인 Backpropagation에 대해서 학습한다. Chain rule에 의거해 여러 상황에서 각각의 weight variable이 cost function에 미치는 영향에 대해 분 석한다. 입력 값이 Real number인 경우와 vector인 경우를 다루며 입력 값이 vector인 경우에 Gradient가 Jacobian행렬이 되는 과정에 대해 분석한다. 또한 기본적인 ANN 구조가 뉴런을 모 방한 것임을 간략하게 설명한다.

Backpropagation

 를 계산해서 가중치 W의 변화가 cost function C 의 변화에 어느정도 영향을 미치는지를 파악해내는 것이다.

Computational Graph (연산 그래프)

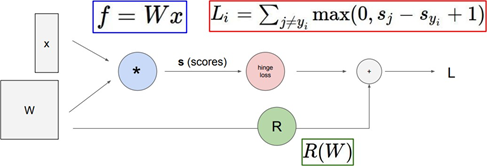
Classifier의 각 연산 과정을 시각화한 그래프다. 연산 과정의 이해를 돕기 위해 사용할 수 있다.

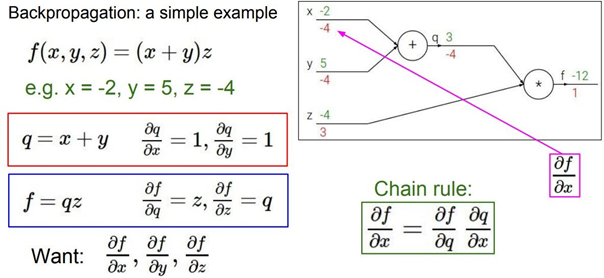
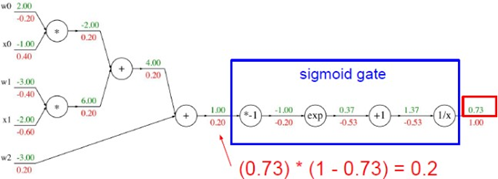
Forward Pass시에 우리는 local gradient를 미리 구해 저장할 수 있다. 이는 backward pass에서 Chain rule을 활용하기 때문인데 최종적인 𝛛𝐟/𝛛𝐱 (gradient)를 구하기 위해 𝛛𝐟/𝛛𝐪라는 global gradient를 역전파과정에서 구해오면 𝛛𝐪/𝛛𝐱라는 local gradient를 곱해줘야 하기 때문이다. 위의 그림에서 𝛛𝒒 의 의미를 파악하는 것이 매우 중요한데 x가 +1변화할 때마다 q에서는 -4만큼 변화한다는 의미로 해석할 수 있다. 따라서 𝛛𝒇/𝛛𝐱 의 의미는 개별적인 변수 x가 전체 함수 f에 미치는 영향을 정량적으로 분석한 것이라고 볼 수 있다. 결국 역전파란 역방향으로 각 Layer의 가중 치가 전체 비용 함수 C(Loss function + Regularization)에 미치는 영향을 수치화한 것이다.

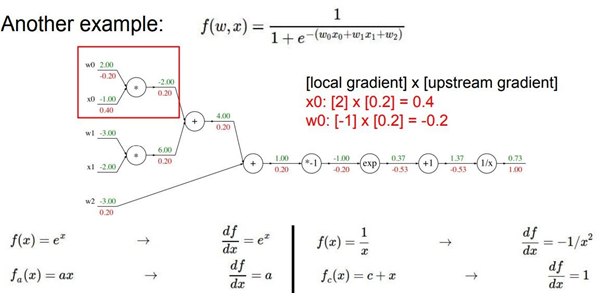
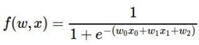
위 예제의 함수를 자세히 보면 \(𝝈(𝒙) = \frac{1}{1+e^{-x}}\) sigmoid function과 매우 유사하다. 입력값 x대신 woxo+w1x1+w2를 집어넣은 것만 다를 뿐 나머지 형태는 똑같다. 여기서 woxo+w1x1+w2는 MLP에서 layer와 layer사이의 연산으로 활성 함수의 입력 값으로 해석할 수 있다. 이 sigmoid function을 미분하면

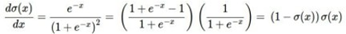
형태가 되는데 여기에 𝝈(𝒙) =0.73(위 예제 참조)를 대입하면 (1-0.73)*0.27=0.2 이다. 즉 함수 전 체를 미분한 후 함수값을 대입해서 나온 미분 값과 chain rule 연산을 통해 도출한 미분 값이 일 치한다는 것을 확인할 수 있다.

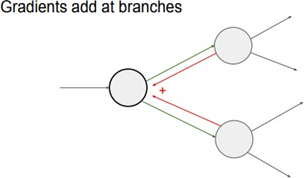
그럼 이제 local gradient는 하나인데 global gradient가 2개인 상황을 상상해보자.

이제 벡터를 연산한다면 어떻게 될지 생각해보자. 변수 x, y, z에 대해서 숫자 대신 vector를 취한다고 가정하면 Gradient는 Jacobian 행렬이 된다. x, y의 각 원소에 대해 z에 대한 미분을 포함하는 행렬이 되는 것이다.

Jacobian matrix

2개의 입력값에 대해서 2개의 출력값이 존재한다면 각각의 f1= x2-y2, f2=2xy에 대해서 x, y로 미분해야 한다. 따라서 벡터함수 f의 i번째 함수를 j번째 변수로 편미분한 도함수를 𝛛𝐟_𝐢/𝛛𝐱_𝐣라 표현하는데 이를 모아서 행렬로 표현하면 Jacobian matrix이라고 한다.

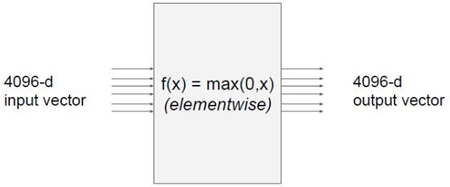
위의 그림은 4096-dim input vector와 4096-dim output vector를 가지는 model이다. 이 노드는 요소별로 최대값을 취해주는데 이 경우 Jacobian 행렬의 사이즈는 어떻게 될까?

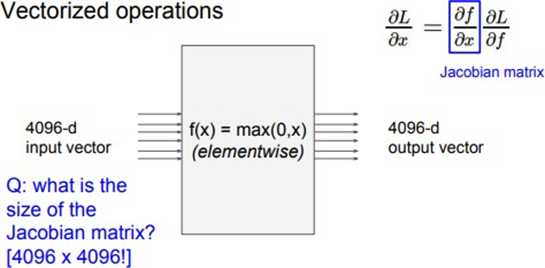
Jacobian matrix의 각 row는 4096가지의 output value에 대해서 존재하는 4096개의 function중 하나를 4096가지의 변수(input value)로 partial derivative(편미분)한 값이다. 즉 첫번째 행은 첫 번째 출력 값을 출력하는 함수 f1을 4096개의 변수에 대해서 partial derivative한 row vector인 것이다. 따라서 Jacobian matrix의 크기는 [4096X4096] size를 갖게 된다. 만약 여기서 100개의 mini-batch를 갖고 있다면 [4096X409600] size를 갖게 된다. Jacobian행렬은 multivariable function의 출력 값에 대한 입력 값의 영향력을 한눈에 파악할 수 있는 도구이다. 또 다른 예시 를 확인해보자.

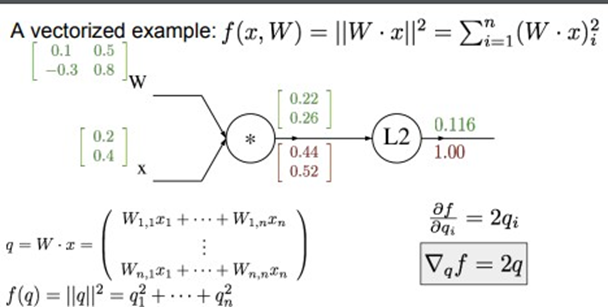
여기선 입력 이미지가 하나라는 가정하에 W^(T)X행렬 곱 연산을 수행하지만 실제 Mini-batch가 input value로 들어와 X가 column vector가 아닌 Matrix가 된 경우, 실제 행렬 곱 연산은 XW형태로 이루어진다. 따라서 두 연산 과정을 모두 고려하는 유연한 관점이 필요하다. 아래의 연산 과정은 행렬곱연산을 기반으로 이루어진 것이다. Backward pass를 시행하면 아래와 같다. \(\frac{𝛛f}{𝛛𝐪} = = 1*2[0.22 0.26]^T = [0.44 0.52]^T\) 따라서 우리가 얻는 것은 경사 0.44와 0.52인 벡터다. 경사의 각 원소는 이 특정 원소가 우리의 함수의 최종 출력에 얼마나 영향을 미치는 지를 의미한다. Q1이 +1되어 1.22가 되면 L2의 함수 값은 1.556이 된다. 0.44만큼 상승하는 것이다.

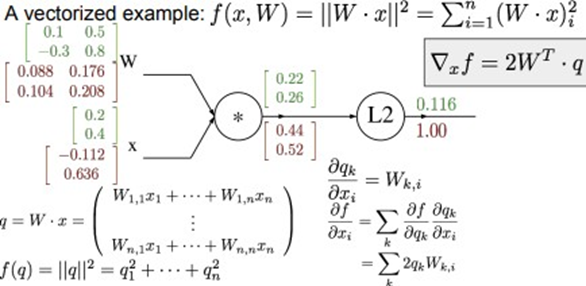
이후 𝛛f/𝛛w 를 구하기 위해 \(\frac{𝛛q}{𝛛w}*\frac{𝛛f}{𝛛q} = 2𝒙^Tq\) 연산을 수행한다. 행렬 곱 연산을 수행하기 위해 행렬x를 전치 행렬로 변환한다. 따라서 2X2행렬이 생성된다. 여기서 각 변수에 대한 gradient를 지속적으 로 체크하는 것이 중요한데 변수에 대한 경사는 변수와 같은 모양을 가져야 하기 때문이다. 마찬가지로 x에 대한 미분도 위의 과정으로 이루어지게 된다. \(\frac{𝛛f}{𝛛x} = \frac{𝛛q}{𝛛w}*\frac{𝛛f}{𝛛q} = 2𝒙^Tq\)

Neural Networks

W가 행렬이고 x가 입력 열 벡터로서 이미지의 모든 픽셀의 값을 가질 때 \(s = W^Tx\) 형태로 class score 연산을 수행했다. 따라서 위의 식을 Linear score function이라고 한다. CIFAR-10의 경우 x는 3072-dim 열 벡터이고 W는 크기가 [10X3072]인 행렬이다. 따라서 output score는 크기가 [10X1]인 vector가 된다. 그러나 만약 Layer가 2개인 Neural Network라 면 어떨까?

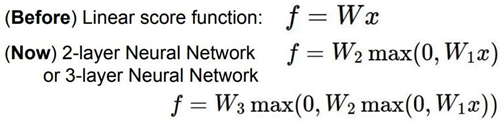
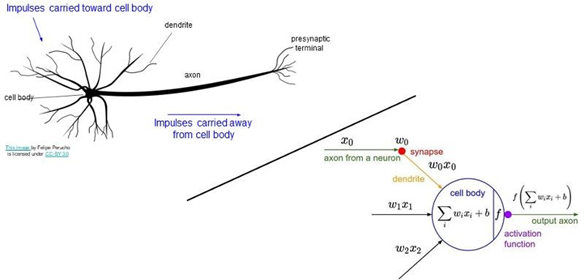
가장 단순한 Artificial Neural Network 형태인 perceptron은 뉴런의 작동방식을 모방한 것이다.